Embark on a captivating journey through the world of geometry with the Big Ideas Geometry Answer Key. This comprehensive guide unlocks the mysteries of geometry, providing you with the knowledge and tools to conquer any geometric challenge that comes your way.

From the fundamental concepts to advanced topics like trigonometry and conic sections, this answer key will guide you through the intricacies of geometry, making it accessible and enjoyable.

Geometry Concepts and Big Ideas

Geometry is a branch of mathematics that deals with the study of shapes, sizes, and spatial relationships. It is a fundamental subject that has been studied for centuries and has applications in a wide variety of fields, including architecture, engineering, and computer science.

The basic concepts of geometry include points, lines, planes, and angles. These concepts are used to define more complex shapes, such as triangles, squares, and circles. Geometry also deals with the relationships between shapes and their properties, such as area, volume, and perimeter.

Relationship with Other Branches of Mathematics

Geometry is closely related to other branches of mathematics, such as algebra and trigonometry. Algebra is used to solve geometric problems involving equations and inequalities. Trigonometry is used to solve geometric problems involving angles and triangles.

Applications in Real-World Situations

Geometry has a wide variety of applications in real-world situations. For example, geometry is used in the design of buildings, bridges, and roads. It is also used in the development of computer graphics and video games. Geometry is even used in the study of nature, such as the shapes of plants and animals.

Geometric Shapes and Properties

Geometry deals with shapes, their properties, and their relationships. Geometric shapes are two- or three-dimensional figures with specific properties. Understanding these shapes and their properties is essential for various fields, including architecture, engineering, design, and science.

Geometric shapes can be classified into different types based on their dimensions, angles, and sides. Some common types of geometric shapes include polygons, circles, spheres, cubes, and pyramids. Each shape has its unique set of properties, such as the number of sides, angles, faces, and edges.

Formulas and Theorems

Formulas and theorems play a crucial role in geometry. They provide mathematical equations and relationships that allow us to calculate the area, perimeter, and volume of geometric shapes. These formulas and theorems are derived from the properties of the shapes and can be used to solve various geometry problems.

• Area:The area of a shape represents the amount of two-dimensional space it occupies. Formulas for calculating the area of different shapes, such as rectangles, triangles, and circles, are essential in geometry.
• Perimeter:The perimeter of a shape represents the distance around its boundary. Formulas for calculating the perimeter of different shapes, such as rectangles, triangles, and circles, are used to determine the length of their boundaries.
• Volume:The volume of a shape represents the amount of three-dimensional space it occupies. Formulas for calculating the volume of different shapes, such as cubes, spheres, and pyramids, are used to determine the amount of space they enclose.

Applications of Geometric Properties

Geometric properties find practical applications in various fields. For instance, in architecture, understanding the properties of shapes is essential for designing buildings, bridges, and other structures. In engineering, geometric properties are used to calculate the strength and stability of structures and machines.

• Construction:Geometric shapes are used to design and construct buildings, bridges, and other structures. The properties of shapes, such as their strength, stability, and aesthetics, are considered during the design process.
• Engineering:Geometric properties are used in engineering to design and analyze machines, vehicles, and other mechanical systems. The properties of shapes, such as their strength, durability, and efficiency, are crucial in engineering design.
• Art and Design:Geometric shapes are used in art and design to create visually appealing and meaningful compositions. The properties of shapes, such as their symmetry, balance, and contrast, are used to create visually pleasing designs.

Geometric Transformations

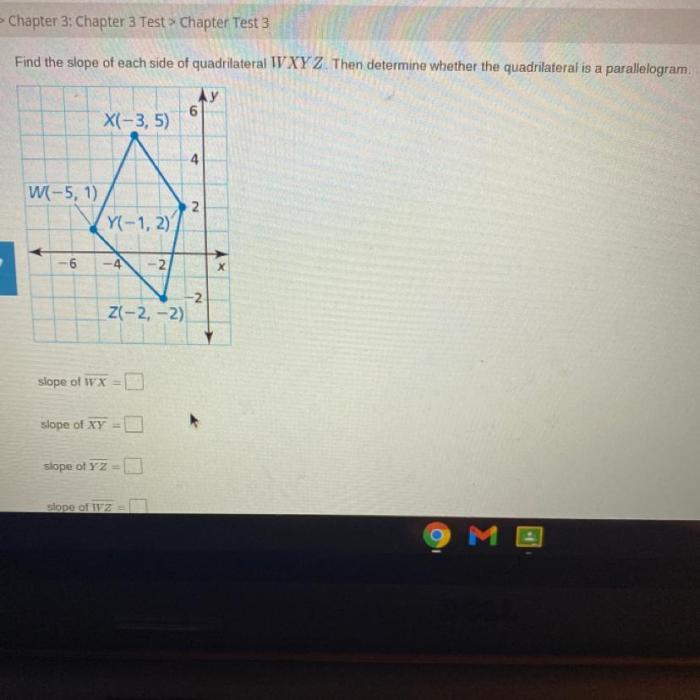
Geometric transformations are mathematical operations that move, flip, or resize geometric shapes. They play a crucial role in geometry, design, and various real-world applications.

There are four main types of geometric transformations: translations, rotations, reflections, and dilations.

Solving geometry problems can be a breeze with the Big Ideas Geometry Answer Key. And did you know that many cities in the US have Spanish names? From Los Angeles to San Antonio, explore the rich Hispanic heritage embedded in these urban landscapes.

Whether you’re a geometry whiz or just curious about the origins of these city names, the Big Ideas Geometry Answer Key and the history of US cities with Spanish names are both fascinating journeys.

Translations

A translation moves a shape from one point to another without changing its size or orientation. It is described by a vector that specifies the direction and distance of the movement.

• Translation preserves the shape and size of the original figure.
• Translation is a rigid transformation, meaning it does not change the shape or size of the figure.
• Translation can be represented by a vector.

Rotations

A rotation turns a shape around a fixed point by a specified angle. It is described by the center of rotation and the angle of rotation.

• Rotation preserves the shape and size of the original figure.
• Rotation is a rigid transformation, meaning it does not change the shape or size of the figure.
• Rotation can be represented by an angle and a center of rotation.

Reflections

A reflection flips a shape over a line, called the line of reflection. It is described by the line of reflection.

• Reflection preserves the shape and size of the original figure.
• Reflection is a rigid transformation, meaning it does not change the shape or size of the figure.
• Reflection can be represented by a line of reflection.

Dilations

A dilation increases or decreases the size of a shape by a specified factor, called the scale factor. It is described by the center of dilation and the scale factor.

• Dilation does not preserve the shape of the original figure, but it does preserve its angles.
• Dilation is not a rigid transformation, meaning it changes the size of the figure.
• Dilation can be represented by a scale factor and a center of dilation.

Coordinate Geometry

Coordinate geometry is a branch of mathematics that uses algebra to represent geometric shapes and their relationships. It is based on the idea of the coordinate plane, which is a two-dimensional plane where each point is identified by two numbers, called coordinates.

The first coordinate, called the x-coordinate, measures the horizontal distance of the point from a vertical line called the y-axis. The second coordinate, called the y-coordinate, measures the vertical distance of the point from a horizontal line called the x-axis.

Types of Equations, Big ideas geometry answer key

There are many different types of equations that can be used to represent geometric shapes. Some of the most common include:

• Linear equations: These equations are in the form y = mx + b, where m is the slope of the line and b is the y-intercept.
• Quadratic equations: These equations are in the form y = ax^2 + bx + c, where a, b, and c are constants.
• Circle equations: These equations are in the form (x – h)^2 + (y – k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.

Applications

Coordinate geometry has many applications in real life. For example, it can be used to:

• Find the distance between two points.
• Find the area of a triangle or a circle.
• Find the perimeter of a rectangle or a square.

li>Plot graphs of functions.

Advanced Geometry Topics

Advanced geometry delves into concepts that extend beyond basic shapes and measurements. It encompasses specialized fields like trigonometry, vectors, and conic sections, each with its unique applications in various disciplines.

Trigonometry

Trigonometry focuses on the relationship between angles and sides of triangles. It’s indispensable in fields like navigation, surveying, and astronomy, where precise angle and distance calculations are crucial. Trigonometric functions (sine, cosine, and tangent) provide the tools to solve complex problems involving angles and triangles.

Vectors

Vectors represent quantities that have both magnitude and direction. They find extensive use in physics and engineering. Vector operations like addition, subtraction, and dot products help analyze forces, velocities, and other physical quantities that have directional components.

Conic Sections

Conic sections arise from intersecting a plane with a cone. They include circles, ellipses, parabolas, and hyperbolas. These curves have remarkable properties and applications in fields like optics, acoustics, and projectile motion. Understanding conic sections is essential for designing optical lenses, parabolic reflectors, and predicting projectile trajectories.

Questions and Answers: Big Ideas Geometry Answer Key

What is the Big Ideas Geometry Answer Key?

The Big Ideas Geometry Answer Key is a comprehensive guide that provides solutions and explanations for all the exercises and problems in the Big Ideas Geometry textbook.

How can I use the Big Ideas Geometry Answer Key?

You can use the Big Ideas Geometry Answer Key to check your answers, review concepts, and prepare for tests.

Is the Big Ideas Geometry Answer Key available online?

Yes, the Big Ideas Geometry Answer Key is available online in various formats, including PDF and ePub.