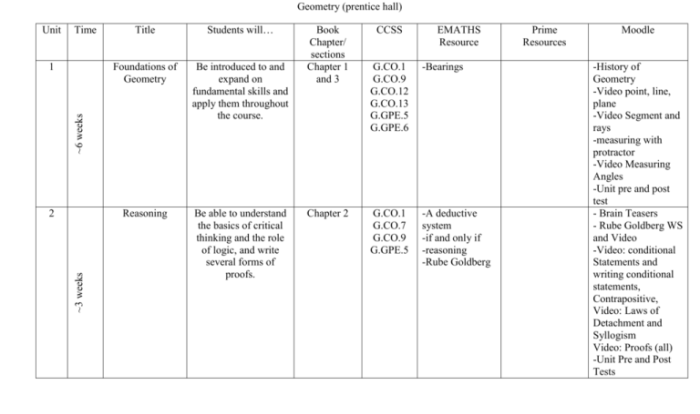
Converse of the pythagorean theorem answer key – The converse of the Pythagorean theorem is a fundamental theorem in geometry that provides a powerful tool for solving problems involving right triangles. In this comprehensive guide, we will explore the statement, proof, applications, common misconceptions, and extensions of the converse of the Pythagorean theorem.

This theorem asserts that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

Definition of the Converse of the Pythagorean Theorem

The converse of the Pythagorean theorem states that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

In other words, if a^2 + b^2 = c^2, then the triangle with sides a, b, and cis a right triangle.

For example, if the sides of a triangle are 3, 4, and 5, then the square of the longest side is 5^2 = 25, which is equal to the sum of the squares of the other two sides, 3^2 + 4^2 = 9 + 16 = 25. Therefore, the triangle is a right triangle.

Proof of the Converse of the Pythagorean Theorem

To prove the converse of the Pythagorean theorem, we can use a geometric construction.

Let ABCbe a triangle with sides a, b, and c. Suppose that a^2 + b^2 = c^2.

Construct a square with side length c. Let the vertices of the square be D, E, F, and G.

Construct a semicircle with diameter DE. Let the center of the semicircle be O.

Draw a line from Oto C. This line will intersect the semicircle at a point H.

Since DEis a diameter of the semicircle, the triangle DHCis a right triangle.

Therefore, by the Pythagorean theorem, we have DH^2 + HC^2 = DC^2.

But DC = cand DH = a, so we have a^2 + HC^2 = c^2.

Similarly, we can show that HC = b. Therefore, we have a^2 + b^2 = c^2, which proves that the triangle ABCis a right triangle.

Applications of the Converse of the Pythagorean Theorem

The converse of the Pythagorean theorem has many applications in various fields, including:

• Architecture:Determining the length of support beams and rafters in buildings.
• Engineering:Calculating the forces and stresses in bridges, towers, and other structures.
• Navigation:Determining the distance between two points on a map or chart.
• Surveying:Measuring the distances between landmarks and determining the area of land.

Common Misconceptions and Pitfalls

There are a few common misconceptions and pitfalls related to the converse of the Pythagorean theorem:

• Misconception:The converse of the Pythagorean theorem is the same as the Pythagorean theorem.
• Pitfall:It is important to remember that the converse of the Pythagorean theorem is only true if the square of one side is equal to the sum of the squares of the other two sides. If this condition is not met, then the triangle is not necessarily a right triangle.

• Misconception:The converse of the Pythagorean theorem can be used to find the area of a triangle.
• Pitfall:The converse of the Pythagorean theorem cannot be used to find the area of a triangle. The area of a triangle can be found using the formula A = (1/2)bh, where bis the length of the base and his the height of the triangle.

Extensions and Related Theorems

There are several extensions and related theorems to the converse of the Pythagorean theorem, including:

• Pythagorean triple theorem:A Pythagorean triple is a set of three positive integers that satisfy the Pythagorean theorem. For example, (3, 4, 5)is a Pythagorean triple because 3^2 + 4^2 = 5^2.
• Distance formula:The distance formula can be derived from the converse of the Pythagorean theorem. The distance formula states that the distance between two points (x_1, y_1)and (x_2, y_2)is given by d = sqrt((x_2- x_1)^2 + (y_2 – y_1)^2) .

Question & Answer Hub: Converse Of The Pythagorean Theorem Answer Key

What is the converse of the Pythagorean theorem?

The converse of the Pythagorean theorem states that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

How can I use the converse of the Pythagorean theorem to solve problems?

You can use the converse of the Pythagorean theorem to determine if a triangle is a right triangle. If the square of one side is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

What are some common misconceptions about the converse of the Pythagorean theorem?

A common misconception is that the converse of the Pythagorean theorem is the same as the Pythagorean theorem. However, the converse of the Pythagorean theorem is a different statement that provides a different condition for determining if a triangle is a right triangle.